THIS POST IS LONG! If you don’t care to see how the answers were calculated and just want to know the size of the 3D area into which all possible Hive games could fit, just skip to the bottom of the post for the results.
While doing secondary-research to get ready for writing AI for our Xbox version of Hive, I noticed that there wasn’t much published about the game-theory for Hive yet. That’s strange for such a popular abstract-strategy game but the game, but I guess someone has to be the first …so it’s going to be us!
This is hopefully the first post in a series which will seek to start more in-depth research on Hive by calculating some of the common measures of the complexity of Hive.
This post is going to show how we calculated the bounding-board for Hive. For a very easy comparison, chess and checkers are played on a square board that has 8 rows and 8 columns and thus has 64 spaces. Since Hive doesn’t have a static board, and instead is created by whatever undirected graph of hexagonal tiles is laid down by the players, calculating the bounding board is less straightforward.
Hive Board Size Calculation – Background
Quick background:
- As shown in the official Hive rules, the basic game has 11 black tiles and 11 white tiles for a total of 22 tiles. Our calculations will refer to this core version of the game without modifications unless noted otherwise.
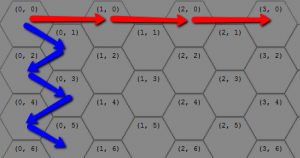
- For the sake of calculations and nomenclature, we’ll be using the coordinate system described in our recent post about representing hexagonal boards in 2-dimensional arrays. This post will be very hard to follow if you haven’t read that.
- Since the Hive board can be reshaped dynamically and could actually be moved end-over-end in any direction indefinitely, there is no actual physical board that you could make which could be used to contain an ongoing game. Rather, the “bounding board” we seek to calculate is the smallest area in which absolutely every legal permutation of board states could be contained. In more simple English: we could use this to make a box such that any legal game of Hive could be covered with this box. If we lift the box and another play is made, we could again cover the board with the box (even if the box is in a slightly different location).
Step 1: Building the bounding board
Now it’s time to start imagining all of the extremes. To make the examples easier to visualize, we will picture all of the white tiles on one side and all of the black tiles on the other side, with their point of contact being the queen from each side. Now we can build the board:
click for fullsize version
-
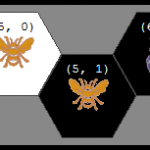 If the tiles were laid out to maximize the number of columns, they would follow a zig-zag pattern from the left to the right. Since each two pieces would equal one-column, then there would be 5 columns taken up by white pieces, then the white queen and black queen would share the center column, followed by 5 more columns of black tiles. This leads to 11 columns. This can be done in 2 rows, but the next example will show that the number of rows used could also be increased.
If the tiles were laid out to maximize the number of columns, they would follow a zig-zag pattern from the left to the right. Since each two pieces would equal one-column, then there would be 5 columns taken up by white pieces, then the white queen and black queen would share the center column, followed by 5 more columns of black tiles. This leads to 11 columns. This can be done in 2 rows, but the next example will show that the number of rows used could also be increased.
-
 To create the most extreme diagonals, interestingly, the number of columns does not decrease at all in this coordinate system. However, when the pieces are laid out so that they are all 45-degrees off from each other, the maximum number of rows now increases to 22.
To create the most extreme diagonals, interestingly, the number of columns does not decrease at all in this coordinate system. However, when the pieces are laid out so that they are all 45-degrees off from each other, the maximum number of rows now increases to 22.
-
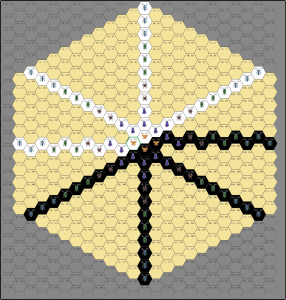 If all of the extreme examples are superimposed upon each other, the minimum bounding-area becomes clear. Awesomely enough, the bounding area is a heaxagon! Patterns everywhere, man. It tickles my math-parts that the hexagon is also rotated 90-degrees from the orientation of the hexagonal tiles themselves.
If all of the extreme examples are superimposed upon each other, the minimum bounding-area becomes clear. Awesomely enough, the bounding area is a heaxagon! Patterns everywhere, man. It tickles my math-parts that the hexagon is also rotated 90-degrees from the orientation of the hexagonal tiles themselves.
Step 2: Measuring the bounding board
Since the board is not a simple square, a bit more math needs to be done in order to calculate the size of the bounding area. This will be done for the general-case of Hive in terms of the number of tiles which each color has available. This gives the bonus of making it trivial to calculate a maximum board-size for the other existing variants to Hive also.
It’s actually pretty easy to calculate the size of the bounding hexagon:
| The number of tiles which each color has will be called “X”. In the default Hive game, for example, there are 11 tiles of each color. |
eg: X = 11 |
| For simplicity, the hexagon can be broken into three parts. Triangle A on top, rectangle B in the middle, and triangle C on the bottom. |
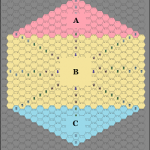 |
| The number of spaces (the area) of the bounding board is just the sum of these parts. |
Area = A + B + C |
| This is a hexagon, so A is just a mirror-image of C, but the size of A and C is the same |
A = C, so
Area = 2A + B |
| The way hexagons get laid out in a triangular shape makes it so that row 1 has 1 tile, row 2 has 2 tiles, etc. Therefore, the area of A is the triangle number of X. We’ll use T(X) to represent the triangle number of X. |
A = T(X) |
| B is a rectangle on the hexagonal grid, so it contains rows whose width fluctuates between being X tiles wide and X-1 tiles wide. Therefore, we can say that B is the sum of the longer rows (which appear on the top and bottom) plus the sum of the narrower rows (of which there is one-fewer because they are neither on the top of the rectangle nor on the bottom). |
Area = 2T(X) + B
B = (sum of pieces in the wider rows) + (sum of pieces in the narrower rows) |
| The wider rows are X+1 tiles wide, and the whole rectangle is X tiles high. |
sum of pieces in the wider rows = ((X+1 tiles) * X rows) |
| The narrower rows are X tiles wide and there is one less row of these because they are bounded on each side by the wider rows. |
sum of pieces in the narrower rows = (X tiles * (X-1) rows) |
| Therefore… |
B = ((X+1) * X) + (X * (X-1)) |
| Substituting that back into the area equation we get… |
Area = 2T(X) + ( ((X+1) * X) + (X * (X-1)) ) |
So that gives us the maximum area of the bottom layer of the minimum bounding board of Hive. Bottom layer, you say? Yup: we haven’t accounted for that wily Beetle yet! For the unacquainted: the Beetle is a special piece in Hive which has the ability to climb on top of other tiles and trap them.
Step 2.5: Modifying the total to take height into account – a.k.a. “What about the Beetle!?”
Since Hive pieces can be stacked, the board is technically 3D: it is a hexagonal prism. Therefore we need the total volume of the board to measure the number of board-spaces.
In Game Theory, it’s most important to create an upper-bound on the number of board spaces (cells), the state-space complexity (number of valid board configurations), and game-tree complexity (all possible moves), rather than necessarily having the exact number. While the calculations shown above for the bottom-layer of the board are exact, when taking height into account we can over-estimate a little (for simplicity) to get a general case equation for the upper-bound of all variants of Hive.
Since the total number of spaces (on all levels) needs to be calculated, the equation can be modified by multiplying the maximum size of a layer by the maximum height the board can achieve. The maximum height that the tiles can achieve will be referred to as H, so the new equation is:
Max board spaces = H * (2T(X) + ( ((X+1) * X) + (X * (X-1)) ))
Step 3: Applying the equation: the actual upper-bound of the Hive board size!
As mentioned above, this is a slight over-counting which we might explain and tweak in a later post, but this will still give us an important start if we just fill in the numbers to the general-case equation above.
Plug and chug:
| General equation derived above |
Max board spaces = H * (2T(X) + ( ((X+1) * X) + (X * (X-1)) )) |
| Hive without any modifications has 11 tiles of each color. |
X = 11 |
| In the basic edition of Hive, the maximum height is achieved by piling all 4 Beetles (2 from each color) on top of the same non-Beetle tile. This maximum height, therefore is 5.
|
H = 5 |
The general equation for Triangle numbers is T(X) = (X * ((X+1)/2)) |
T(11) = (11 * ((11+1)/2))
T(11) = 66 |
| Substitute these values in |
Max board spaces = 5 * ((2*66) + ( ((11+1) * 11) + (11 * (11-1)) )) |
| The maximum possible number of board-spaces in the smallest bounding region which could contain any legal configuration of a game of Hive with no modifications: |
Max board spaces in Hive = 1,870 |
So there you have it, there are no more than 1,870 spaces in the virtual board for Hive. For comparison, chess (which is pretty complex already) has 64 spaces.
Did you have as much fun with that as I did? 😀
Please comment if you’ve looked over my reasoning and it seems solid, if you’ve found some errors to correct, or if you have any questions.
Thanks!
Update: In the comments, Hive Champion, Randy Ingersoll, helps narrow it down to 1,290 spaces in the virtual board for Hive.
 BlueLine Games is a small team and we NEED to move fast (time is money!). Because of this we need awesome (and lightweight) project managment solutions.
BlueLine Games is a small team and we NEED to move fast (time is money!). Because of this we need awesome (and lightweight) project managment solutions.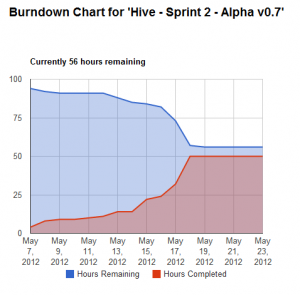 2012-05-23 Update: Tonight I’ve released an upgrade to switch from the old Google Image Charts API (which is deprecated now and will disappear in 11 months) to the new Google Charts API. In simple english: the charts now look better, they have mouse-over info on every point, and they have two lines (“Hours Elapsed” and “Hours Completed”).
2012-05-23 Update: Tonight I’ve released an upgrade to switch from the old Google Image Charts API (which is deprecated now and will disappear in 11 months) to the new Google Charts API. In simple english: the charts now look better, they have mouse-over info on every point, and they have two lines (“Hours Elapsed” and “Hours Completed”).